Travail de préparation

Sur la figure -1-, un poids « m2 » est représenté immergé dans le champ gravitationnel, acquérant un mouvement. Il entraîne, via un fil inextensible, un mobile autoporteur de masse « m1 » qui glisse sur un rail sans frottement. On néglige la masse de la poulie ainsi que le frottement du fil passant dans sa gorge.

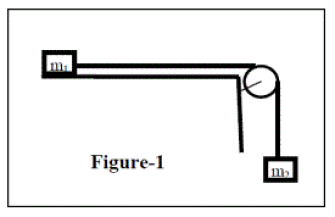
Fig 2 : Le mouvement du système constitué des deux masses

1- Faire l'inventaire des forces extérieures appliquées au mobile autoporteur de masse « m1 » et au poids «m2» dans la figure -1-

  • Réponse :

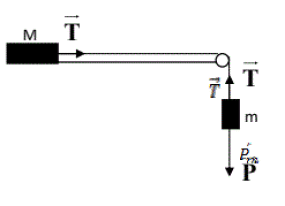
Fig 3 : l'inventaire des forces extérieures

2- Appliquer la deuxième loi de Newton au mobile autoportant (m1) et au poids (m2)

  • Réponse :

∑ F 1 ⃗ = m 1 a ⃗ et ∑ F 2 ⃗ = m 2 a ⃗ sum widevec { F_{1}}= m_{1} widevec {a} et sum widevec { F_{2}}= m_{2} widevec {a}

3-En les projetant sur différents axes. Écrivez les équations de force pour chaque masse

  • Réponse :

T 1 = m 1 ∗ a P 2 − T 2 = m 2 ∗ a T 1 = T 2 P 2 = m 2 ∗ g P 1 = m 1 ∗ g stack{stack{T_{1}= m_{1}*a # P_{2}-T_{2}= m_{2}*a # T_{1}= T_{2}} # P_{2}=m_{2}*g #P_{1}=m_{1}*g }

4- Dérivé l'expression littérale de l'accélération (a) du système en fonction de m1, m2 et g

  • Réponse :

a = m 2 m 1 + m 2 ⋅ g a= { m_{2}} over { m_{1}+ m_{2}} cdot g

5-Quel est le type de mouvement ?

  • Réponse :

    Mouvement rectiligne uniformément variable (MRUV) (accélération)

6-Donner l'équation temporaire de ce mouvement

  • La réponse :

S = 1 2 ∗ a ∗ t 2 + V 0 ∗ t + S 0 S= {1} over {2}*a* t^{2}+ V_{0}*t+ S_{0}