Informatique 1

Le système décimal est basé sur la numération de base 10, ce qui signifie qu'il utilise dix symboles différents pour représenter les valeurs de 0 à 9. Chaque position dans un nombre décimal a une valeur qui est une puissance de 10. Par exemple, dans le nombre 365, le chiffre 5 est dans la position des unités, le chiffre 6 est dans la position des dizaines et le chiffre 3 est dans la position des centaines.

Le système binaire est largement utilisé dans les systèmes informatiques car il est basé sur la numération de base 2. Il utilise seulement deux symboles, 0 et 1, pour représenter toutes les valeurs. Chaque position dans un nombre binaire a une valeur qui est une puissance de 2. Par exemple, dans le nombre binaire 1011, le chiffre 1 est dans la position des unités, le chiffre 1 est dans la position des deux, le chiffre 0 est dans la position des quatre et le chiffre 1 est dans la position des huit.

Le système octal est basé sur la numération de base 8. Il utilise huit symboles différents, de 0 à 7, pour représenter les valeurs. Chaque position dans un nombre octal a une valeur qui est une puissance de 8. Le système octal est moins courant dans les applications modernes, mais il était largement utilisé dans les premiers systèmes informatiques.

Le système hexadécimal est basé sur la numération de base 16. Il utilise seize symboles différents, de 0 à 9 puis de A à F (représentant les valeurs 10 à 15), pour représenter les valeurs. Chaque position dans un nombre hexadécimal a une valeur qui est une puissance de 16. Le système hexadécimal est souvent utilisé dans les applications informatiques pour représenter des nombres binaires de manière plus concise et lisible.

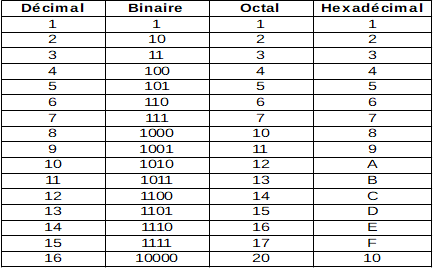
Ce tableau illustre la conversion des chiffres de 1 à 16 entre les systèmes décimal, binaire, octal et hexadécimal. En observant ce tableau, vous pouvez remarquer comment les chiffres sont représentés différemment dans chaque système, mais conservent leur valeur fondamentale. Cela démontre l'importance et la flexibilité des systèmes de codage des informations dans le domaine de l'informatique et de la technologie en général.

Les systèmes de complément sont des techniques utilisées en informatique pour effectuer des opérations arithmétiques sur des nombres binaires de manière efficace. Parmi ces systèmes, on trouve le complément à un et le complément à deux.

Le premier complément, également connu sous le nom de complément à un, est une méthode simple pour représenter les nombres négatifs en binaire. Dans ce système, pour obtenir le complément à un d'un nombre binaire, il suffit d'inverser tous les bits du nombre original, c'est-à-dire remplacer chaque 0 par un 1 et chaque 1 par un 0. Le principal inconvénient de cette méthode est qu'elle entraîne un double zéro (0) pour la représentation du nombre zéro, ce qui complique les opérations arithmétiques.

Le deuxième complément, également appelé complément à deux, est une amélioration du complément à un. Pour obtenir le complément à deux d'un nombre binaire, on commence par prendre le complément à un du nombre, puis on ajoute 1 au résultat. Par exemple, pour obtenir le complément à deux de 5 en binaire (101), on prend d'abord le complément à un (010) et ensuite on ajoute 1 pour obtenir (011). Cette méthode permet de représenter efficacement les nombres négatifs tout en évitant le problème du double zéro, car le zéro est représenté de la même manière que dans le système de valeurs positives.