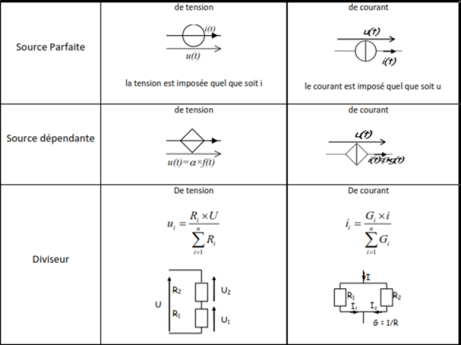
Association de dipôles

On dit les dipôles quelconques sont dits associés en série si une des bornes de l'un est reliée à une des bornes de l'autre, l'ensemble formant un nouveau dipôle.

Ils sont dits associés en parallèle si les paires de bornes sont connectées deux à deux (figure I.7).

Dans le cas de l'association de dipôles sont en série s'ils sont parcourus par la même intensité de courant électrique. La tension totale aux bornes de l'ensemble est égale à la somme des deux différences de potentiel aux bornes de chacun des deux dipôles.

Et ils sont en de dipôles en parallèle s'ils ont une même différence de potentiel à leurs bornes

Association de dipôles actifs

Le dipôle équivalent à l'association en série de n générateurs de tension de résistances internes rk et de force électromotrice Ek est un générateur de tension unique.

Figure I.8 : Association de dipôles actifs

Association de dipôles passifs

Fondamental

L'association des récepteurs passifs dans un circuit électrique permet de créer des configurations spécifiques pour diviser le courant et la tension, augmenter ou diminuer la résistance, la capacité ou l'inductance

Rappel

L'association de dipôles passifs est la combinaison de composants électriques tels que les résistances, les condensateurs et les bobines dans un circuit pour obtenir des caractéristiques électriques spécifiques, telles que la modification de la tension, du courant ou de l'impédance.

Association des résistances en série

La résistance équivalente d'un groupement des résistances en série est égale à la somme des résistances montées en série

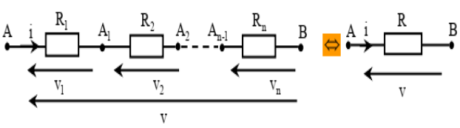
Figure 1.9 : Groupement des résistances en série

On a donc :

U = ∑ K n U K = ∑ K n R K ⋅ I = R ⋅ I U= sum from{K} to{n} U_{K} = sum from{K} to{n} R_{K} cdot I= R cdot I

par conséquent on obtient:

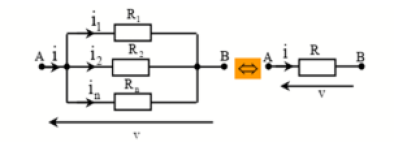
R = ∑ k n R K = R 1 + R 2 ...... R n R= sum from{k} to{n} R_{K}= R_{1}+R_{2}......R_{n}
Association des résistances en parallèle :

L'inverse de la résistance équivalente d'un groupement des résistances en parallèle est égal à la somme des inverses des résistances montées en parallèle.

1 R = ∑ k n 1 R K = 1 R 1 + 1 R 2 ....... 1 R n {1} over {R} = sum from{k} to{n} {{1} over {R_{K}} } = {1} over {R_{1}}+{1} over {R_{2}}.......{1} over {R_{n}}
Figure 1.10 : Groupement des résistances en parallèle
Association des inductances en série :

'inductance équivalente d'un groupement des inductances en série est égale à la somme des inductances montées en série. On a donc :

L K = ∑ k n L K = L 1 + L 2 ...... L n L_{K}= sum from{k} to{n} L_{K}= L_{1}+L_{2}......L_{n}
Figure 1.11 : Groupement des inductances en série
 Association des inductances en parallèle :

L'inverse de l'inductance équivalente d'un groupement en parallèle des inductances est égal à la somme des inverses des inductances.

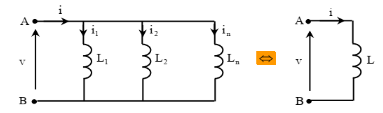
Fig.1.12 : Groupement des inductances en parallèle

On a donc :

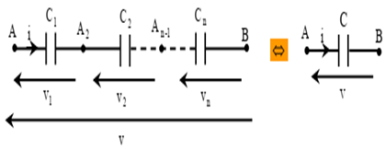
1 L = ∑ k n 1 L K = 1 L 1 + 1 L 2 ....... 1 L n {1} over {L} = sum from{k} to{n} {{1} over {L_{K}} } = {1} over {L_{1}}+{1} over {L_{2}}.......{1} over {L_{n}}
Association des condensateurs en série :

L''inverse de la capacité équivalente d'un groupement en série des capacités est égal à la somme des inverses des capacités. On a donc :

1 C = ∑ k n 1 C K = 1 C 1 + 1 C 2 ....... 1 C n {1} over {C} = sum from{k} to{n} {{1} over {C_{K}} } = {1} over {C_{1}}+{1} over {C_{2}}.......{1} over {C_{n}}
Figure 1.13: Groupement en parallèle des capacités

Remarque

Attention

On remarquera que les règles d'associations des résistances et celles d'associations des condensateurs se trouvent inversées.