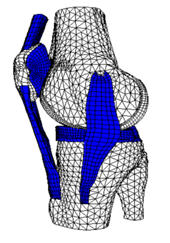
La résolution des équations différentielles ou plus
généralement des équations aux
dérivées
partielles occupe une place importante en ingénierie et en mathématiques
appliquées.
Chacune de ces disciplines apporte une contribution différente mais
complémentaire
à la compréhension et à la résolution de tels problèmes.
Il
existe plusieurs techniques permettant de résoudre les équations aux dérivées
partielles.
On pense par exemple aux méthodes de différences finies, de volumes finis,
aux
méthodes spectrales, etc. On peut sans aucun doute affirmer que la plus
largement
répandue
est la méthode des éléments finis. Cette popularité n’est pas sans fondement.
La
méthode des éléments finis est très générale et possède une base mathématique
rigoureuse
qui est fort utile, même sur le plan très pratique. En effet, cette base
mathématique
permet de prévoir jusqu’à un certain point la précision de notre
approximation
et même d’améliorer cette précision, via les méthodes adaptatives.
- معلم: Noureddine MENASRI
1- Fiche de contact :
Photo
Titre de la matière : Éléments Finis (Methodologie)
Faculté :Technologie
Département : Génie Mécanique
Cycle : 1èr année Master
Semestre :
1 (2)
Crédits : 4
Coefficients : 2
Volume : 3h (1h30)
Enseignant : Menasri Noureddine
Email :noureddine.menasri@univ-msila.dz.
- معلم: Noureddine MENASRI
Objectifs de l’enseignement:
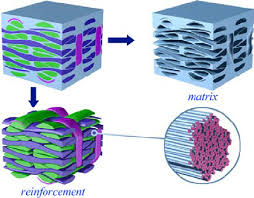
Concevoir et développer des matériaux composites à matrice polymère en choisissant la
matrice adaptée, le type de renfort (focus sur la fibre de carbone) et le procédé d'élaboration
à mettre en œuvre pour obtenir des propriétés spécifiques et contrôlées.
Tirer partie de l'association dans un matériau composite d’une matrice polymère continue et
de renforts pour produire un effet de synergie entre les propriétés des différents éléments
constitutifs
Contribuer au développement de composites en respectant un cahier des charges typique des
applications industrielles les plus courantes.
Le cours thermodynamique et diagrammes d'équilibres est destiné aux étudiants de génie des matériaux Master 1
- معلم: ZEMMAMOUCHE Redouane
Cette matière traite l’aspect de la mécanique des matériaux notamment les matériaux métalliques, et comporte plusieurs parties. Elle commence par les essais mécaniques simple comme la traction, la dureté, la résilience et d’autre essais qui présentent des lois simples et donnent à l’étudiant les définitions des différents paramètres mécaniques. L’objectif de cette première partie est d’étudié l’élasticité et la plasticité des matériaux. La loi de Hooke qui détermine le coefficient d’élasticité est généralisé aux d’autres coefficients par une étude générale des états de contrainte et de déformation. La mise en forme des matériaux par déformation plastique impose la connaissance des modèles de comportement plastique, c’est le but de la deuxième partie de cette matière. Le comportement des matériaux fragiles comportant des fissures est un savoir indispensable pour un étudiant en génie des matériaux. Une introduction à la mécanique de la rupture linéaire est présentée dans la troisième partie de ce cours, cette partie permet d’illustrer à l’étudiant la particularité du comportement des matériaux fragiles.
- معلم: Younes BENARIOUA
