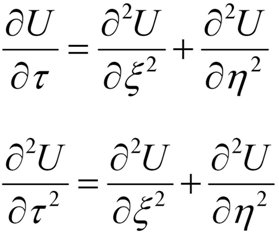Létude et la résolution des EDPs dévolution repose sur plusieurs méthodes , il ya tout
dabord létude dexistence et de lunicité de la solution, où on utilise les méthodes classiques
telle que le point
xe ou méthode de compacité.
En suite il ya les méthodes numériques pour chercher des solutions approchées, où on
utilise par exemple la méthode de di¤érences
nies où autres méthodes.
En
n il ya les méthode de recherche de solutions particulières exactes ou approchées,
les solutions approchées sont sous la forme dune série par exemple. ar contre pour les
solutions particulières exactes
on peut citer les solutions dites "solutions auto-similaires".
la recherche de solutions analytiques exactes ou approchées est interressante pour com-
parer en analyse numérique avec la solution calculée et aussi dans le cas théorique pour voir
le comportement de la solution étudiée.
Les solutions auto-similaires jouent un grand rôle dans l
مقرر مقياس المعادلات التفاضلية غير الخطية لطلبة السنة أولى ماستر رياضيات تخصص EDP
- معلم: abdelhak mokhtari
Différences finies pour EDPs d'évolution
Dans ce cous on s'intéresse aux équations aux dérivées partielles elliptiques linéaires. Notre objectif est d'analyser la question d'existence, d'unicité et de la régularité des solutions pour cette famille de problèmes en se basant sur la méthode variationnelle. Plus précisément, on commence par donner un rappel sur les espaces de Sobolev et leurs propriétés, la formule de Green, l’inégalité de Poincaré, le , Théorème de Lax-Milgram et le Théorème de Stampacchia. En appliquant les théorèmes précédent pour démontrer l’existence et l’unicité des solutions en se basant sur la formulation variationnelle des quelques problèmes bien choisis.
Référence : Grégoire ALLAIRE - François ALOUGES, Analyse variationnelle des équations aux dérivées partielles, Polycopié du cours MAP 431, École Polytechnique, 16 janvier 20.