Méthodes numériques pour l'optimisation avec contraintes (2024/2025)

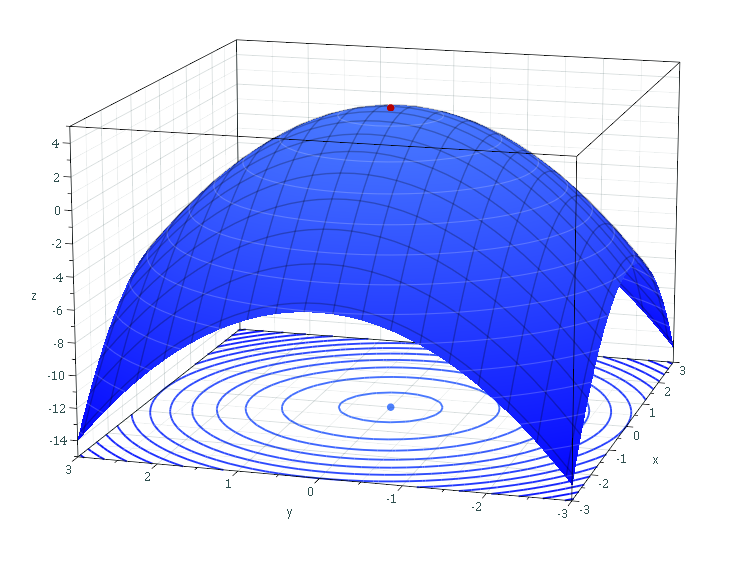
Les problèmes d’optimisation peuvent être rencontrés dans toutes les disciplines et dans de nombreux domaines d’activité. En fonction du contexte, il s’agit de maximiser un "gain" ou de minimiser un "coût" en faisant le "meilleur" choix possible dans un ensemble de variables de décision qui peut être plus ou moins large, plus ou moins contraint. Ce qui peut s’écrire : on cherche x* solution de Min f(x) où x est un variable de C, telle que f est la fonction minimiser et la variable x est à choisir dans l’ensemble des valeurs admissibles C.Un problème de maximisation revient à considérer la minimisation de -f. Lorsque l’ensemble C est un sous-ensemble fermé de Rn , Il s’agit d’un problème d’optimisation avec contraintes. L’objectif de ce cours est de couvrir les méthodes numériques de base pour «résoudre » les problèmes d’optimisation avec contraintes. Ce cours est destiné aux étudiants de:

Niveau: Master 1, Semstre 2

Option: AMN.