Aperçu des sections

  • Généralités

    Tout replier Tout déplier

    L'intelligence artificielle occupe une place singulière dans le champ très vaste de l'informatique, Automatique et l'Electronique et d'autres disciplines bien connues. Alors même que l'intelligence artificielle n'a jamais connu autant de développements et d'applications variés, ses résultats restent largement méconnus dans leur ensemble, y compris dans la communauté des chercheurs. Cette matière décrit quelques problèmes et méthodes associant intelligence artificielle, reconnaissance des formes et apprentissage. La convergence de ces domaines va en s'amplifiant, et ce cours en fournit quelques illustrations. La première partie porte sur les principes généraux :de la reconnaissance structurelle de formes et d'objets et apprentissage. La deuxième partie traite les méthodes de classification directes, Méthodes de coalescence, Méthodes statistiques, Méthodes structurelles, Introduction à l'apprentissage non supervisé, Modèles connexionnistes mono et multi, Introduction aux machines SVM et finalement la combinaison de classifieurs faibles.

             

    Merci à tous ceux, étudiants, enseignants ou lecteurs occasionnels, qui voudront bien me signaler les erreurs, m'indiquer des lacunes ou me faire part de leurs remarques et suggestions de tous genres.


  • Fiche de Contact



    Faculté: Technologie

    Département: Génie Electrique

    Spécialités : Robotique (Master Pro)

    Intitulé du cours : Apprentissage artificiel et reconnaissance des formes

    Crédit: 04

    Coefficient: O2

    Volume horaire : 01 cours (01H.30) & TD/TP (01H.30) 

    Responsable de Cours : Prof. LADJAL Mohamed

    Contact par mail : mohamed.ladjal@univ-msila.dz

    Disponible toute la semaine


  • Objectif de la matière



    L'objectif est de donner aux étudiants les fondements théoriques et méthodologiques en reconnaissance des formes. Ce cours aborde des méthodes modernes d’apprentissage artificiel tel que les approches bayesiénne, les Machines à Vecteurs Supports et la combinaison de classifieurs faible par boosting. Ces algorithmes sont au coeur de nombreuses applications : analyse automatique d'images, reconnaissance de la parole, biométrie, interaction Homme-Robot, bio-informatique...


    TP

    Mettre en pratique et donner un aspect concret aux notions vues au cours "Apprentissage artificiel et reconnaissance des formes" par des travaux pratiques pour mieux comprendre et assimiler le contenu de cette matière


  • Pré-requis


    Traitement des images, traitement du signal

  • Chapitre 1

    Principes généraux : représenter puis classer, global versus structurel, modéliser versus discriminer, généralisation, sur-apprentissage, régularisation, validation croisée, représentation des données, analyse de données, sélection de variables.


  • Chapitre 2 : Méthodes de classification directes : k-plus-proches-voisins

    En reconnaissance de forme, l'algorithme des k plus proches voisins (k-NN) est une méthode non paramétrique utilisée pour la classification et la régression. Dans les deux cas, il s'agit de classer l'entrée dans la catégorie à laquelle appartient les k plus proches voisins dans l'espace des caractéristiques identifiées par apprentissage. Le résultat dépend si l'algorithme est utilisé à des fins de classification ou de régression :

    • en classification k-NN, le résultat est une classe d'appartenance. Un objet d'entrée est classifié selon le résultat majoritaire des statistiques de classes d'appartenance de ses k plus proches voisins, (k est un nombre entier positif généralement petit). Si k = 1, alors l'objet est affecté à la classe d'appartenance de son proche voisin.
    • en régression k-NN, le résultat est la valeur pour cet objet. Cette valeur est la moyenne des valeurs des k plus proches voisins.

    La méthode k-NN est basée sur l'apprentissage préalable, ou l'apprentissage faible, où la fonction est évaluée localement, le calcul définitif étant effectué à l'issue de la classification. L'algorithme k-NN est parmi les plus simples des algorithmes de machines learning.

    Par exemple, dans un problème de classification, on retiendra la classe la plus représentée parmi les k sorties associées aux k entrées les plus proches de la nouvelle entrée x.



  • Chapitre 3 : Introduction aux machines SVM

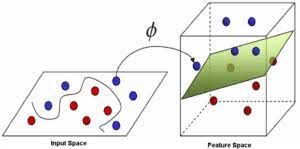
    Les machines à vecteurs de support ou séparateurs à vastes marges (en anglais Support Vector Machines, SVM) sont une classe d’algorithmes d’apprentissage statistique initialement définis pour la discrimination. Destinées à résoudre des problèmes de discrimination et de régression, les SVMs sont considérées comme étant une généralisation des classifieurs linéaires. Cette méthode fût introduite par V. Vapnik à partir de 1995 sur le développement d’une théorie statistique de l’apprentissage appelée théorie de Vapnik-Chervonenkis. Son succès est justifié par les solides bases théoriques qui la soutiennent. Elle permet en fait d’aborder un grand nombre de tâches de classification supervisée telles que : la catégorisation automatique de textes, la reconnaissance de visages, les diagnostics médicaux, la reconnaissance des chiffres manuscrits etc. La méthode SVM est une technique de classification discriminative très populaire, particulièrement bien adaptée au traitement des données de très haute dimension, tels que les textes et les images. Depuis son introduction dans le domaine de la reconnaissance de formes, plusieurs travaux ont pu montrer son efficacité. Fortement basée sur la théorie, il existe en fait un lien direct entre la théorie de l’apprentissage statistique et son algorithme d’apprentissage. Ce dernier suscite un vif intérêt dans la communauté « Machine Learning (ML) » pour ces bonnes performances, et le fait qu’il trouve une solution unique. Toutefois, la véritable force de la méthode reste au niveau du mécanisme de projection qui lui permet de changer d’espace pour réaliser l’apprentissage. 


  • Introduction à l'apprentissage non supervisé, cartes auto-organisantes.

    Le SOM est un réseau de neurones à une seule couche avec des cellules placées le long d'une grille à n dimensions. La plupart des applications utilisent des grilles bidimensionnelles et rectangulaires, bien que beaucoup utilisent également des grilles hexagonales et des espaces à une, trois ou plusieurs dimensions. SOM produit une image projetée à faible dimension d'une distribution de données à haute dimension dans laquelle des relations similaires entre des éléments de données sont préservées.

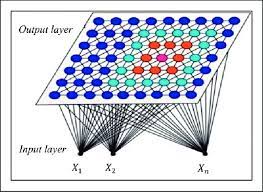
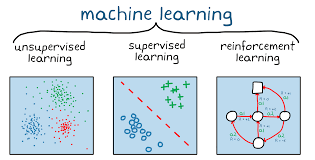
    Apprentissage non supervisé : Contrairement à l'apprentissage supervisé, cet apprentissage non supervisé est aussi appelé « apprentissage compétitif » où seules les valeurs d'entrée sont disponibles. Dans ce cas, les exemples présentés à l'entrée amènent le réseau à générer de manière adaptative des valeurs de sortie proches en réponse à des valeurs d'entrée similaires.





  • Modèles connexionnistes mono et multi, Réseaux bouclés, Régression

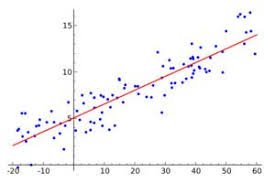
    On utilise la régression lorsque la variable d’intérêt est quantitative, c’est à dire « à valeur » dans un espace métrique – la métrique est une notion de distance définie dans l’espace – et souvent « à valeur continue ». Par exemple on peut essayer de prédire l’âge d’un utilisateur en fonction de son comportement ; l’âge est une donnée continue avec la métrique usuelle des nombres réels


  • TP 1 Initiation Matlab et classification

  • TP 2 kppv

  • TP 3 Prédiction linéaire et non linéaire

  • TP4 Sélection de variable

  • TP 5 Cross Validation

  • Section 14

  • Références bibliographiques


    1. K. Fukunaga, Introduction to Statistical Pattern Recognition (Second Edition),

    Academic Press, New York, 1990.

    2. P.A. Devijver and J. Kittler, Pattern Recognition, a Statistical Approach, Prentice Hall,

    Englewood Cliffs, London, 1982.

    3. R.O. Duda and P.E. Hart, Pattern classification and scene analysis, John Wiley & Sons,

    New York, 1973. (A second edition is being prepared by David Stork).

    4. J.R. Quinlan, C4.5: Programs for machine learning, Morgan Kaufmann Publishers, San

    Mateo, California, 1993.

    5. L. Breiman, J.H. Friedman, R.A. Olshen, and C.J. Stone, Classification and regression

    trees, Wadsworth, California, 1984.


  • Corrigé Type 2022/2023