Modélisation des courbes
Dans l'ordinateur, représenter des objets est important pour différentes disciplines comme la réalité virtuelle, la conception assistée par ordinateur ou la fabrication assistée par ordinateur. La modélisation géométrique des objets est une étape nécessaire où on décrit ces objets avec des formules mathématiques pour effectuer des opérations comme la réunion, l'intersection ou le complément. Cela permet de les représenter graphiquement, que ce soit des éléments simples comme des courbes, surfaces, ou volumes, ou des éléments composés par la combinaison de ces éléments simples. Les débuts de cette discipline remontent aux années 1960 avec des pionniers tels que J. Ferguson et S. Coons aux États-Unis, et P. de Casteljau et P. Bézier en France, qui ont travaillé dans des industries comme Boeing, Ford, Citroën, et Renault. Ce chapitre propose une introduction à la modélisation géométrique en examinant certaines propriétés des courbes.
Fondamental :
Étant donnés n points (de R2 ou de R3), trouver une courbe passant
• par les points => interpolation
• près des points => lissage ou interpolation
Courbes de Bézier
Une courbe de Bézier est une courbe définie mathématiquement par des points de contrôle. Elle porte le nom du mathématicien français Pierre Bézier, qui l'a popularisée dans les années 1960. La courbe est créée en interpolant (liant) les points de contrôle de manière à former une forme lisse et courbée. La courbe de Bézier peut être de différents degrés, en fonction du nombre de points de contrôle utilisés.
Les courbes de Bézier sont largement utilisées en modélisation géométrique, en conception assistée par ordinateur (CAO) et en animation graphique. Elles offrent une manière flexible de définir des formes complexes avec un contrôle précis sur la courbure et la trajectoire. En plus des courbes de Bézier, il existe également des surfaces de Bézier, qui étendent le concept aux formes bidimensionnelles.
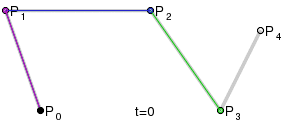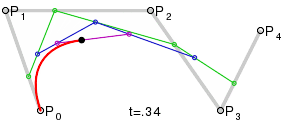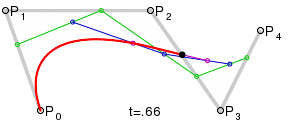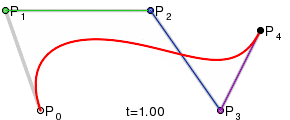
Définition : Définition mathématique
La courbe de Bézier pour les n+1 points de contrôle (P0, ..., Pn), est l'ensemble des points définis par la représentation paramétrique
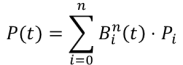
"pour t ∈ [0 ; 1] et où les " B_i^n " sont les polynômes de Bernstein"
Remarque :
Puisque les polynômes de Bernstein forment une partition de l'unité, on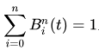
. La somme des coefficients est donc non nulle pour tout t, donc tous les points P(t) de la courbe sont correctement définis.
Propriétés
La courbe est à l'intérieur de l'enveloppe convexe des points de contrôle.
La courbe commence par le point P0 et se termine par le point Pn, mais ne passe pas a priori par les autres points de contrôle qui déterminent cependant l'allure générale de la courbe.
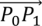est le vecteur tangent à la courbe en P0 et 
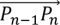au point Pn.La courbe de Bézier est un segment si et seulement si les points de contrôle sont alignés.
Chaque restriction d'une courbe de Bézier est aussi une courbe de Bézier.
Un arc de cercle ne peut pas être décrit par une courbe de Bézier, quel que soit son degré.
Une courbe de Bézier d'ordre 2 est un fragment de parabole si les points qui la définissent ne sont pas alignés.
Le contrôle de la courbe est global : modifier un point de contrôle modifie toute la courbe, et non pas un voisinage du point de contrôle.
Pour effectuer une transformation affine de la courbe, il suffit d'effectuer la transformation sur tous les points de contrôle.
Courbe de Bézier (Videos)
Exemple :
Exemple de Courbe de Bézier
Exemple :
Exemple de Courbe de Bézier بالعربي
Courbes Spline
Définition :
Une courbe spline est une fonction mathématique définie par morceaux à l'aide de polynômes. Elle est utilisée dans divers domaines tels que l'analyse numérique, le lissage de données expérimentales, la conception graphique et la représentation numérique de contours complexes.
Les courbes splines sont des outils puissants pour modéliser des formes complexes de manière lisse et continue. Elles sont largement utilisées dans les domaines de l'informatique graphique, de la CAO (conception assistée par ordinateur) et de l'analyse numérique.
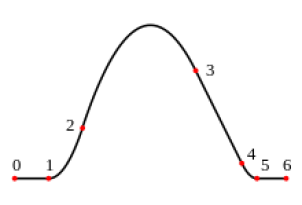
Types de Splines
Il existe plusieurs types de splines, chacun ayant ses propres caractéristiques. Les types de splines les plus courants sont les splines linéaires, cubiques et B-spline. Les splines linéaires sont le type de spline le plus simple, et sont utilisées pour interpoler des lignes droites. Les splines cubiques sont utilisées pour interpoler des courbes et sont composées de polynômes de degré trois. Les splines B sont plus complexes que les splines linéaires et cubiques, et sont composées de polynômes par morceaux de degré variable.
Définition mathématique
Pour définir une spline S de degré k il nous faut n points et n−1 polynômes qi de degré k. La spline est alors définie de la manière suivante :
Propriétés
Définition par morceaux : Une spline est une fonction définie par morceaux, composée de plusieurs segments polynomiaux. Chaque segment est défini sur un intervalle spécifique.
Lissage : Les courbes splines sont conçues pour être lisses. Cela signifie que leurs dérivées sont continues jusqu'à un certain ordre. Cette propriété permet d'éviter les discontinuités et de créer des courbes agréables à l'œil.
Ordre de la spline : L'ordre d'une spline détermine le degré du polynôme utilisé pour chaque segment. Les splines cubiques (degré 3) sont les plus couramment utilisées, car elles offrent un bon équilibre entre flexibilité et simplicité.
Conditions aux limites : Les conditions aux limites définissent les valeurs des dérivées aux extrémités de la spline. Les conditions les plus courantes sont les conditions de Hermite (dérivées première et seconde) et les conditions de Catmull-Rom (dérivée première).
Interpolation : Les splines peuvent être utilisées pour interpoler des points de contrôle. Cela signifie qu'elles passent exactement par ces points, ce qui est utile pour la modélisation de courbes complexes.
B-splines : Les B-splines sont une forme particulière de courbes splines. Elles sont largement utilisées dans la conception assistée par ordinateur (CAO) et l'informatique graphique.
En résumé, les courbes splines sont des outils puissants pour modéliser des formes complexes de manière lisse et continue. Elles sont utilisées dans des domaines tels que l'animation, la conception de formes, le rendu graphique et bien d'autres encore.
Exemple : Courbe Spline Video بالعربي
Courbe Spline بالعربي
Courbes NURBS (Non-uniform rational B-spline)
Les courbes NURBS (Non-Uniform Rational Basis Splines) sont des représentations mathématiques utilisées en infographie et en modélisation 3D pour décrire des courbes et des surfaces lisses.
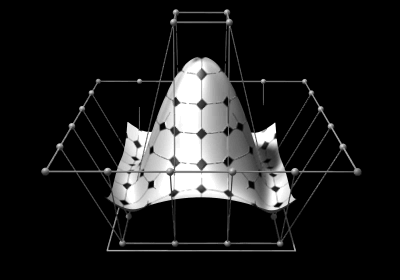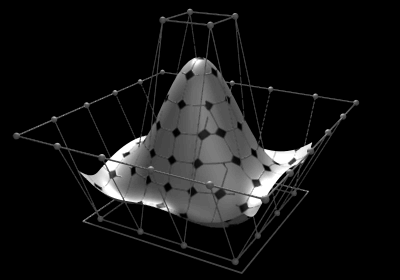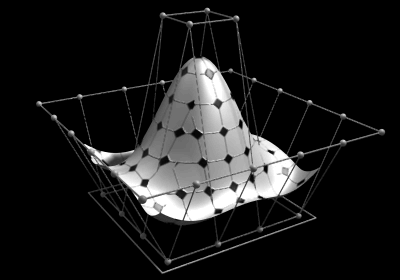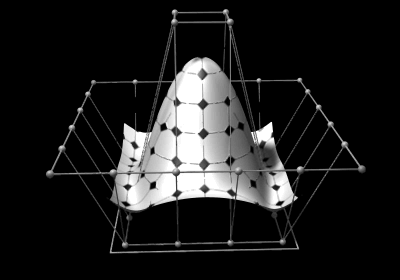
Définition :
Les courbes NURBS sont définies par des points de contrôle et des poids affectés à chacun de ces points.
Elles passent entre les points de contrôle et par les points d'interpolation.
Contrairement aux B-splines uniformes, les NURBS peuvent ajuster des courbes plus complexes et harmonieuses.
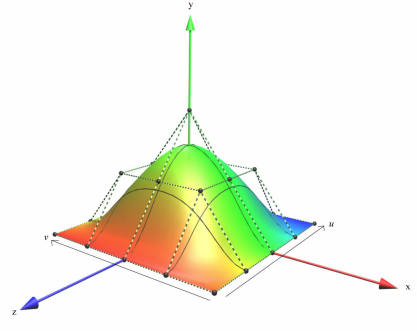
Avantages
Facilité et précision pour évaluer une forme ;
Capacité pour approximer des formes complexes ;
Simplicité de construction et d'implémentation ;
Faible complexité des algorithmes utilisés.
Définition mathématique
La formule d'une courbe NURBS est illustré de la manière suivante :
où les ωi sont les poids des coordonnées homogènes des points de contrôle donnés Pi, m le nombre de nœuds, n
le degré de la NURBS, les coefficients calculés selon l'algorithme de Cox-de Boor, et .
Exemple :
Courbe NURBS Video بالعربي
Conclusion
Les courbes jouent un rôle essentiel dans la modélisation et la CAO (Conception Assistée par Ordinateur) des formes complexes. Voici comment elles contribuent :
1. Représentation des formes :
Les courbes permettent de décrire des formes variées, qu'elles soient 2D ou 3D.
Elles servent à modéliser des contours, des profils, des bords et des surfaces.
Par exemple, dans la conception de pièces mécaniques, les courbes définissent les contours des pièces.
2. Surface et volume :
En reliant des courbes, on peut créer des surfaces complexes.
Les surfaces sont utilisées pour modéliser des objets tridimensionnels.
Les courbes sont les éléments de base pour générer des surfaces et des volumes.
3. Interpolation et approximation :
Les courbes permettent d'interpoler (relier) des points de contrôle pour créer des formes lisses.
Elles sont également utilisées pour approximer des formes complexes à partir de données discrètes.
4. Animation et rendu :
Dans l'animation 3D, les courbes définissent les trajectoires des objets en mouvement.
Elles contrôlent les mouvements des personnages, des caméras et des lumières.
Les courbes sont essentielles pour créer des animations fluides et réalistes.
5. Courbes NURBS :
Les courbes NURBS (Non-Uniform Rational Basis Splines) sont largement utilisées en CAO.
Elles offrent une flexibilité pour modéliser des surfaces complexes avec des propriétés de lissage.
Les NURBS sont couramment utilisées dans des logiciels tels que AutoCAD, SolidWorks et Rhino.
En somme, les courbes sont des éléments fondamentaux pour représenter, modéliser et animer des formes complexes dans le domaine de la CAO et de la modélisation 3D.