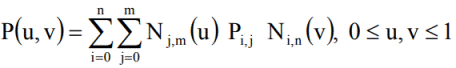Techniques et méthodes de modélisation

Il existe différentes approches et techniques de modélisation des surfaces, et voici quelques-unes des méthodes couramment utilisées :

MéthodeSurfaces Bézier :

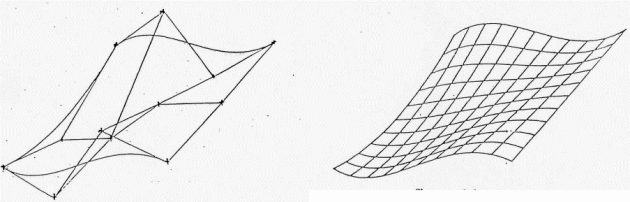
Les courbes de Bézier et les surfaces de Bézier sont largement utilisées dans la modélisation graphique. Elles sont définies par des points de contrôle qui déterminent la forme de la courbe ou de la surface.

On utilise les polynômes de Bézier comme fonctions de mélange :

Surfaces BézierInformations[1]

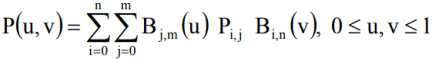
RemarqueAvantages :

  • interprétation aisée des points de contrôle

  • bon contrôle de la surface

Inconvénients :

  • le degré du polynôme est dépendant du nombre de points de contrôle

  • le contrôle de la courbe est global

MéthodeSurfaces B-splines :

Les surfaces B-splines sont une généralisation des surfaces de Bézier, offrant une plus grande flexibilité.

bs-type-1bs-type-2bs-type-3
Clamped, Closed and Open B-spline Surfaces

RemarqueAvantages :

  • le degré du polynôme est indépendant du nombre de points de contrôle

  • le contrôle de la courbe est local

Inconvénients :

  • La surface ne passe par aucun point de contrôle

MéthodeSurfaces NURBS

Une surface NURBS est définie par une combinaison pondérée de fonctions B-splines dans deux directions. Les poids ajoutent une souplesse supplémentaire en permettant de contrôler l'influence de chaque point de contrôle sur la forme finale de la surface.

Les surfaces NURBS s'obtiennent par extension de la définition des courbes NURBS :

– deux vecteurs de nœuds T et S, un pour chacune des variables t et s,

– (m+1) x (n+1) points de contrôle Pi,k

– (m+1) x (n+1) fonctions de pondération Rm,n.i,k déduites des fonctions de pondération des B-splines Sm,k au moyen de (m+1) x (n+1) poids wi,k :

R m , n , i , k ( t ) = w i , k S m , i ( t ) S n , k ( s ) ∑ j , l w j , l S m , j ( t ) S n , l ( s ) , N ( t , s ) = ∑ j , k R m , n , i , k ( t ) P i , k , ( t , s ) ∈ [ 0,1 ] 2 R_{m,n,i,k}(t)= { w_{i,k} S_{m,i}(t) S_{n,k}(s)} over { sum from{j,l} w_{j,l} S_{m,j}(t) S_{n,l}(s) }, N( t,s)= sum from{j,k} R_{m,n,i,k}(t) P_{i,k}, ( t,s) in [0,1] ^{2}

Surfaces NURBSInformations[2]

Propriétés

  • Flexibilité: Représentation de formes complexes allant des simples surfaces planes aux formes organiques.

  • Lissage: Génération de surfaces lisses et continues, sans angles brusques.

  • Contrôle local: Modification de la forme de la surface en ajustant les points de contrôle et leurs poids.

  • Degré: Le degré des fonctions B-splines définit la courbure maximale de la surface.

RemarqueAvantages :

  • Facilité de création et de manipulation de surfaces complexes.

  • Représentation précise des formes géométriques 3D.

  • Largement utilisées dans la CAO et la FAO pour la conception, la simulation et la fabrication

Inconvénients :

  • Les surfaces NURBS peuvent être plus lourdes en termes de calcul que les surfaces B-splines.

  • Processus de conversion des surfaces NURBS en maillages polygonaux pour le rendu, peut être coûteuse en temps et en ressources.

  • La conversion des surfaces NURBS en formats de maillage peut entraîner une perte de précision.