مخطط الموضوع

  • Fiche de contact

    طي الكل توسيع الكل


    Faculté : Sciences

    Département : Chimie

    Public cible : Deuxième licence (L2)

    Intitulé du cours : Méthode Numériques Et Programmation (MNP)

    Crédit : 3

    Coefficient : 2

    Semestre : 01

    Cours : 1h30/Semaine

    TP : 1h30/Semaine

    Unité d’enseignement : Méthodologie – Code : UEM12

    Durée :15 Cemaines  

    Enseignant :

    Cours, TP : Dr. Raghdi Amina

    Contact : par mail au amina.raghdi@univ-msila.dz


  • objectif méthode numérique et programmation

    Le module MNP vise à étudier et à mettre en pratique diverses méthodes numériques pour résoudre des problèmes mathématiques complexes. Alors que les méthodes analytiques offrent des solutions exactes pour certains problèmes, les méthodes numériques sont utilisées lorsque les solutions exactes ne sont pas possibles. Ces méthodes fournissent des solutions approximatives mais souvent précises, et leur mise en œuvre manuelle est difficile voire impossible, nécessitant ainsi la programmation sur ordinateur. Le module se concentre sur l'utilisation du logiciel Matlab, largement utilisé dans le calcul numérique, pour implémenter et résoudre ces méthodes. Les étudiants apprennent à sélectionner et à appliquer les méthodes numériques appropriées pour résoudre des équations, des systèmes d'équations, des équations différentielles, des intégrales, et d'autres problèmes mathématiques, en développant ainsi leurs compétences en résolution de problèmes et en programmation


  • Contenu de cours

    Ce module est structuré en cinq chapitres :

    Chapitre I : Initiation à Matlab (TP)

    Chapitre II : Intégration numérique (Cours et TP)

    1. Méthode des Trapèzes

    2. Méthode de Simpson

    Chapitre III : Résolution numérique des équations non-linéaires (Cours et TP)

    1. Méthode de Bissection

     2. Méthode de Newton

    Chapitre IV : Résolution numérique des équations différentielles ordinaires (Cours et TP)

    1. Méthode d'Euler

    2. Méthode de Runge-Kutta

    Chapitre V : Résolution numérique des systèmes d'équations linéaires (Cours et TP)

    1. Méthode de Gauss

    2. Méthode de Gauss-Seide


  • Introduction

    Le méthode numérique permet de résoudre des problèmes de physique et de mathématiques au moyen du calcul arithmétique sous forme d'algorithmes. On utilise les méthodes numériques quand la résolution analytique du problème est complexe ou impossible, par exemple si on veut résoudre une équation non linéaire du type 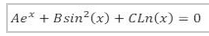  . On a recourt aussi à ces méthodes quand la résolution d'un problème est trop complexe et demande beaucoup de calculs, par exemple le calcul par les méthodes classiques du déterminant d'une matrice d'ordre 50 demande 50! opérations c.‐à‐d. 3 1064 opérations. Si on utilise un ordinateur capable d'exécuter 1000 millions d'opérations seconde, le temps de calcul serait 9x1047 années !

    Aux 18ème et 19ème siècles, les chercheurs tels que Gauss, Fourier et Newton ont développé des algorithmes adaptés au calcul manuel. Après 1945 et avec l'apparition des ordinateurs, les chercheurs se sont intéressés à de nouveaux algorithmes pour une utilisation avec des ordinateurs.


  • Prérequis

    Pour assurer un bon déroulement des travaux dirigés, il est nécessaire de posséder :

    -       Quelques notions mathématiques.

    -          Langage de programmation C++, fortran et MATLB



  • chapitre 01 : Intégration numérique.

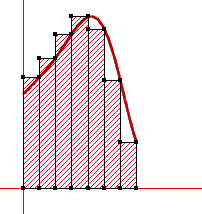
    Objectif : Maîtriser les méthodes d'intégration numérique, telles que la méthode des trapèzes et la méthode de Simpson, pour calculer des intégrales numériques avec précision


  • Chapitre 2 : Résolution Des Equations Non Linéaires

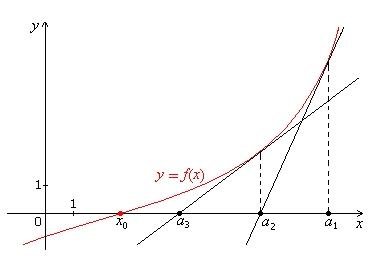
    objectif Apprendre à résoudre numériquement des équations non linéaires en utilisant la méthode de la bissection et la méthode de Newton


  • test de sortie

                                                                                                                     

  • référence


    Pour les méthodes numériques

    1.  F. JEDRZEIJEWSKI, Introduction aux méthodes numériques, 2ème Ed., Springer, France, (2005).

    2. J. HOFFMAN, Numerical methods for engineers and scientists, 2nd Ed, Marcel Dekker, USA, (2001).

    3.  A. QUARTERONI, Méthodes numériques, algorithmes, analyse et appl., Springer, Italie, (2004).

    Pour MATLAB

    1.  M. DJEBLI & H. DJELOUAH, Initiation à MATLAB, OPU, (2013).

    2.  R. DUKKIPATI, MATLAB, an introduction with applications, New Age International Publishers, India, (2010).

    3. C. WOODFORD and C. Phillips, Numerical methods with worked examples: MATLAB edition, 2 nd Ed. Springer Ltd, (2013).