E-learning -Université de M'sila
نتائج البحث: 5241
1- La résolution des équations différentielles ou plus
généralement des équations aux
dérivées
partielles occupe une place importante en ingénierie et en mathématiques
appliquées.
Chacune de ces disciplines apporte une contribution différente mais
complémentaire
à la compréhension et à la résolution de tels problèmes.
Il
existe plusieurs techniques permettant de résoudre les équations aux dérivées
partielles.
On pense par exemple aux méthodes de différences finies, de volumes finis,
aux
méthodes spectrales, etc. On peut sans aucun doute affirmer que la plus
largement
répandue
est la méthode des éléments finis. Cette popularité n’est pas sans fondement.
La
méthode des éléments finis est très générale et possède une base mathématique
rigoureuse
qui est fort utile, même sur le plan très pratique. En effet, cette base
mathématique
permet de prévoir jusqu’à un certain point la précision de notre
approximation
et même d’améliorer cette précision, via les méthodes adaptatives.
Module destiné aux 2éme année master transport et mobilité urbaine
- معلم: TAHRAOUI lyes

fiche descriptive de module

Semestre : 1
Unité d’enseignement : UEM1.1
Matière 2 : Méthodes expérimentales
VHS : 22h30 (Cours : 1h30)
Crédits: 2
Coefficient : 1
Objectifs de l’enseignement:
Cette matière apporte à l’étudiant des connaissances sur les développements les plus récents concernant les essais courants de la mécanique des sols, surtout au laboratoire et aussi sur le terrain.
Cours méthodes numériques pour les étudiants de département de génie éléctrique 2 eme année licence
- معلم: kehali salima
Résolution des équations non linéaires f(x)=0 (3 semaines)
Introduction sur les erreurs de calcul et les approximations, Introduction sur les methodes de resolution des equations non lineaires, Methode de bissection, Methode des approximations successives (point fixe), Methode de Newton-Raphson.
Ce Module est réservé pour la présentation des différentes méthodes et techniques numériques dans le but de faire :
- Exposer et acquérir un ensemble de méthodes numériques permettant de résoudre des problèmes impossibles par des approches analytiques.
- Savoir transposer la connaissance mathématique pure à un ordinateur aux performances finies.
- Résoudre numériquement des problèmes dont la solution analytique est connue ou non.
- Analyser le comportement des méthodes.
Le contenu de ce document est destiné aux étudiants en Master de l'électromécanique (ELM) au département de génie électrique à l’université de Mohamed Boudiaf M’sila. Il s’inspire de nombreux ouvrages et références bien plus complets, ainsi que divers documents de collègues universitaires. Ce document est bien sur incomplet : il manque des chapitres entiers, des démonstrations, des exemples, etc. Toute remarque est la bienvenue, même en ce qui concerne les probablement nombreuses fautes d’orthographes.
- معلم: salah belkhiri

 Chapitre 1 :
Chapitre 1 :
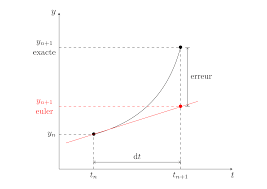
Equations du 1er ordre, développement en série de Taylor, Méthode d’Euler et propagation de l’erreur, Méthodes de Runge-Kutta et appréciation des erreurs, systèmes d’EDO, méthodes à pas multiples, méthode de prédiction-correction. Application aux équations de couches limites écoulement et convection forcées et naturelle sur plaques planes.
- معلم: nadjib baadji

coefficient 2, credit 3, 45h+ 30h travail complémentaire
méthode d'evaluation 50% control continu, 50% examen
contenu:
references
- Pour FORTRANUEM12 / M122TP Optique Géométrique & Physique(1h30’ TP/ sem. ou 3h TP/15j) ; 22h30’/SemestreUEM12 / M123Méthodes Numériques et Programmation(1h30’ Cours + 1h30’ TD ou TP/semaine) ;45h00/Semestre
- -B. HAHN, ‘’Introduction to Fortran 90 for scientists and engineers’’, Capetown University, SouthAfrica, (1993).-Ph. D’Anfray, ‘’Fortran 77’’, Université Paris XIII, (1998).-P. CORDE et A. FOUILLOUX, Langage Fortran, Support de cours, IDRIS, (2010).Pour les méthodes numériques-F. JEDRZEIJEWSKI,Introduction aux méthodes numériques, 2èmeEd., Springer-Verlag, France,(2005).-E. HAIRER, Introduction à l’analyse numérique, université de Genève, (2001).-J. HOFFMAN, Numerical methods for engineers and scientists, 2ndEd, Marcel Dekker, USA,(2001).-A. QUARTERONI,Méthodes numériques, algorithmes, analyse et applications, Springer-Verlag,Italie, (2004)
Apprendre à l’étudiant les approximations de la solution des équations différentielles ordinaires et d’équations différentielles aux dérivées partielles. Celles-ci ont plusieurs applications en énergie solaire, mecanique des fluides ainsi que le transfert de chaleur.
- معلم: Hichem BOULECHFAR
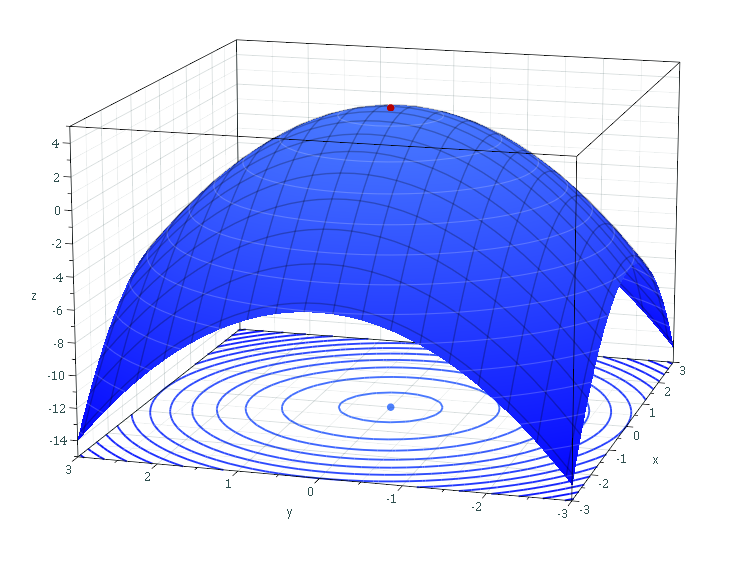
Les problèmes d’optimisation peuvent être rencontrés dans toutes les disciplines et dans de nombreux domaines d’activité. En fonction du contexte, il s’agit de maximiser un "gain" ou de minimiser un "coût" en faisant le "meilleur" choix possible dans un ensemble de variables de décision qui peut être plus ou moins large, plus ou moins contraint. Ce qui peut s’écrire : on cherche x* solution de Min f(x) où x est un variable de C, telle que f est la fonction minimiser et la variable x est à choisir dans l’ensemble des valeurs admissibles C.Un problème de maximisation revient à considérer la minimisation de -f. Lorsque l’ensemble C est un sous-ensemble fermé de Rn , Il s’agit d’un problème d’optimisation avec contraintes. L’objectif de ce cours est de couvrir les méthodes numériques de base pour «résoudre » les problèmes d’optimisation avec contraintes. Ce cours est destiné aux étudiants de:
Niveau: Master 1, Semstre 2
Option: AMN.

- معلم: ahmed bahloul
- معلم: seifeddine drif
Le mémoire de Master est un exercice d’initiation à la recherche dans lequel le candidat traite un sujet (peut être original) sous la direction d’un enseignant chercheur. La phase de recherches se conclut par la rédaction d’un mémoire, qui est ensuite soutenu devant un jury. Il représente un exercice de synthèse qui met en œuvre les savoirs et savoir-faire des enseignements d’un cycle entier (L ou M), ou plus précisément de certains modules de cette formation.
On peut dire aussi, le mémoire est un exercice difficile car il constitue une nouveauté dans votre cursus. Si vous êtes arrivé en master 2, c’est que vous avez déjà fait vos preuves : vous avez des bases solides en Mathématiques, vous maîtrisez les outils principaux de démonstration et de conclusion. Tout cela vous sera encore très utile.
Le mémoire doit montrer la capacité du candidat à poser une problématique, développer des argumentations et maîtriser une bibliographie : il doit connaître l’état d’une question et faire avancer la recherche.
Les conseils Méthodologiques que vous trouverez ici sont toutefois à moduler en fonction du sujet, de l’étudiant et du directeur de mémoire. Et bien entendu, votre guide principal sera votre directeur de mémoire. En aucun cas, les conseils mentionnés dans le présent guide ne viennent se substituer à ceux que votre directeur de mémoire pourra vous prodiguer tout au long de la préparation du mémoire.
- معلم: lemnaouar zedam


