Logique Algébrique
Aperçu des sections
-
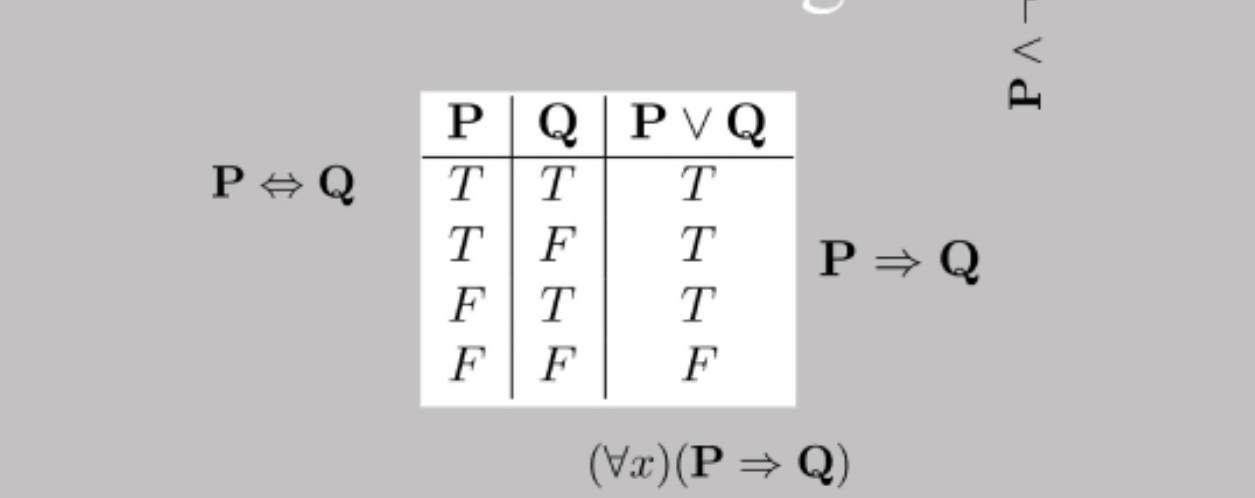
-
- Faculty: Mathematics and Computer Science
- Department: Mathematics
- Target Audience : 2nd year Master
Course title: Logique Algèbrique
Credit : 04
- Coefficient : 02
- Duration : 14 seasons
- Hour: 1H30 courses and 1h30 TD
- Instructor : Dr Kheir Saadaoui
- Contact : kheir.saadaoui@univ-msila.dz
-

This course is designed to provide a deep dive into some of the foundational and advanced topics in mathematics that are essential for understanding complex systems and decision-making processes
-
This chapter explores the foundational concepts of ordered sets and lattices. You'll learn about the structure of sets where order matters, such as how elements relate to each other in a hierarchy. We'll also delve into lattices, which are special ordered sets that allow us to find common ancestors and descendants of elements
-
In this chapter, we investigate the fascinating world of logic beyond true and false. Łukasiewicz trivalent algebras introduce a third value: undetermined. This extension of classical logic helps us model scenarios where information is incomplete or uncertain
-
This chapter introduces fuzzy sets, which allow for a more nuanced classification of elements. Unlike classical sets with strict boundaries, fuzzy sets handle degrees of membership, making them ideal for dealing with uncertainty and imprecision in real-world situations.
-
Here, we delve into triangular norms (T-norms) and conorms (T-conorms), essential tools in fuzzy logic and probability theory. These operations extend the concepts of logical AND and OR to the realm of fuzzy sets
-
This chapter focuses on how fuzzy sets can represent the structures and operations of Łukasiewicz trivalent algebras
-
-
Fichier
-
